2 乱数

Exercise 2.1 R言語の組み込み関数runifを用いて，長さ\(1000\)の疑似一様乱数\(x_1, x_2,\ldots, x_{1000}\)を生成せよ．また，それらを\(1\times 1\)の二次元正方形に配置せよ，すなわち， \(xy\)平面上に，\(\{(x_1, x_2), (x_3, x_4), \ldots, (x_{999}, x_{1000})\}\)を描画せよ．

u <- matrix(runif(1000),nrow=2)
data.fr <- data.frame(x=u[1,], y=u[2,])
ggplot(data.fr,aes(x=x,y=y))+geom_point()+theme_bw()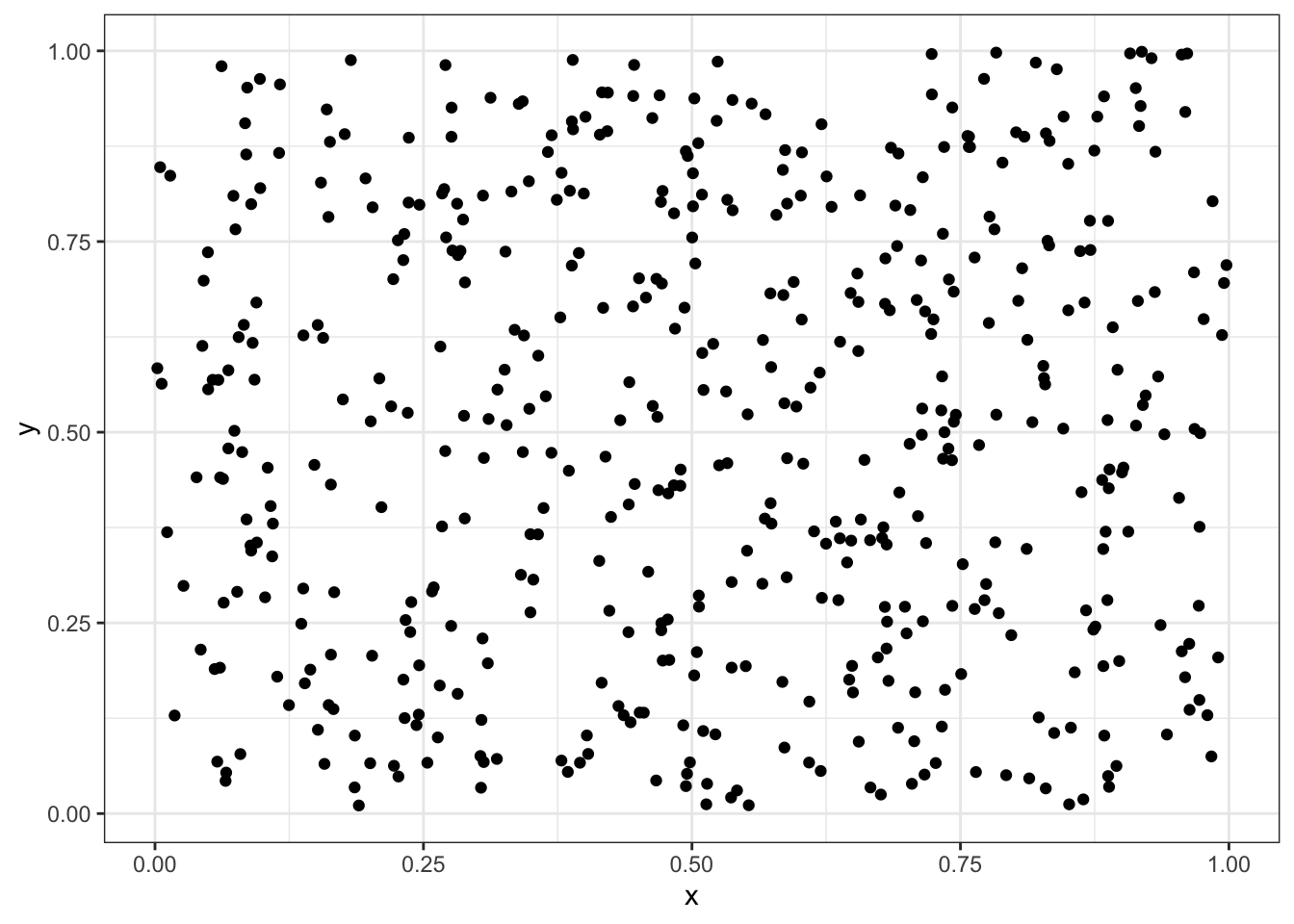

なお，三次元への配置は次のようにしてできる．

set.seed(1234)
x <- runif(1e3)
y <- runif(1e3)
z <- runif(1e3)
plot_ly(x=x, y=y, z=z, type="scatter3d", mode="markers", size=0.1)

さらに，RAND法の配置は次のようにすれば良い．三次元に配置すると問題が起きることも見える．

u <- numeric(3*1e3)
y <- 1234
n <- 2 ^ 31 - 1
a <- 65539
b <- 0

for(i in 1:length(u)){
  y <- (a * y + b) %% n
  u[i] <- y/n
}

u_mat <- matrix(u, nrow=3)
x <- u_mat[1,]
y <- u_mat[2,]
z <- u_mat[3,]
plot_ly(x=x, y=y, z=z, type="scatter3d", mode="markers", size=0.1)

Exercise 2.2 \(a=13, b=0, n=67\)とし，初期値\(y_0=1234\)として線形合同法を用いて，長さ\(1000\)の疑似一様乱数\(x_1, x_2,\ldots, x_{1000}\)を生成せよ．また，上の問題と同じように，それらを\(1\times 1\)の二次元正方形に配置せよ，また，描画された点のうち，異なる点の数を数え上げよ．

u <- numeric(1e3)
y <- 1234
n <- 67
a <- 13
b <- 0
for(i in 1:length(u)){
  y <- (a * y + b) %% n
  u[i] <- y/n
}

u_mat <- matrix(u, nrow=2)
data.fr <- data.frame(x=u_mat[1,], y=u_mat[2,])
ggplot(data.fr,aes(x=x,y=y))+geom_point()+theme_bw()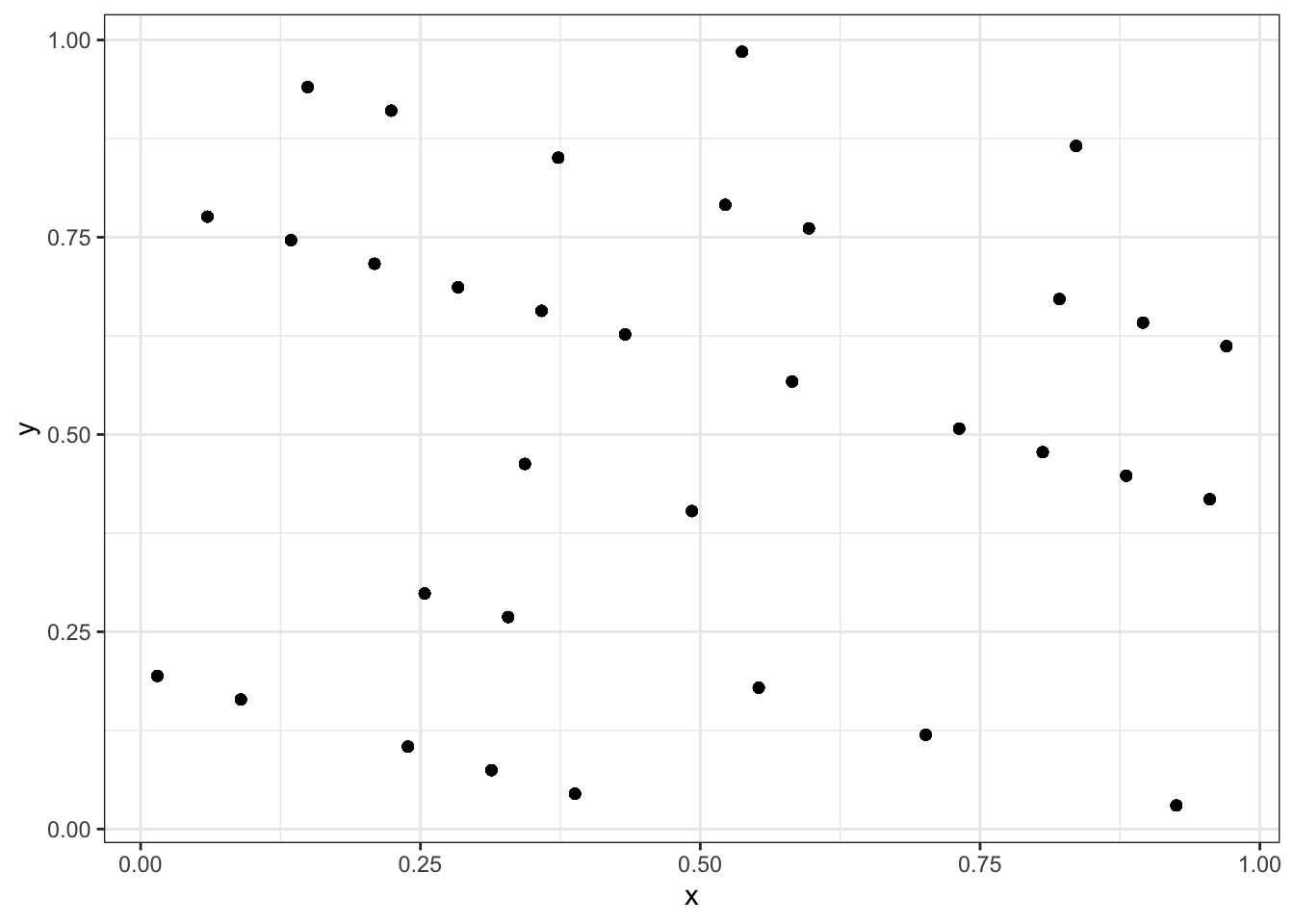

dim(unique(data.fr))[1] #No. of unique points

## [1] 33

Exercise 2.3 ロジスティック分布 (Logistic distribution)は \[\begin{equation}\nonumber%\label{eq:logistic_function} F(x)=\frac{e^x}{1+e^x}\ (-\infty<x<\infty) \end{equation}\] なる累積分布関数を持つ．R言語の組み込み関数runifを使ってロジスティック乱数を生成せよ．また，R言語の組み込み関数rlogisと計算時間の比較をおこなえ．

Solution. 逆変換法を使おう．累積分布関数の逆関数は \[ F^{-1}(u)=\log \frac{u}{1-u} \] だから，\(U\sim\mathcal{U}[0,1]\)なら\(F^{-1}(U)\)がロジスティック分布に従う．

f <- function(u){ return(log( u / (1 - u) ) )}
N <- 1e5
microbenchmark(A <- f(runif(N)), times = 100)

## Unit: milliseconds
##              expr      min       lq     mean   median       uq      max neval
##  A <- f(runif(N)) 3.804779 3.952959 4.617068 4.276453 4.717159 10.36159   100

microbenchmark(B <- rlogis(N), times = 100)

## Unit: milliseconds
##            expr      min       lq     mean   median       uq      max neval
##  B <- rlogis(N) 3.626015 3.927983 4.256843 4.084026 4.377028 8.237903   100

組み込み関数が\(10\%\)ほど速いようだ．

Exercise 2.4 \(a, b\)を正の実数とする．パレート分布 (Pareto distribution) の確率密度関数が \[ p(x;a,b)=\frac{ab^a}{x^{a+1}}\ (x\ge b) \] で与えられるとき，R言語の組み込み関数runifを用いてパレート乱数を生成する方法を記述せよ．

Solution. まず累積分布関数を計算しよう．定義どおり積分すると，任意の\(x\ge b\)に対し \[\begin{align*} F(x)&=\int_b^xp(y;a,b)\mathrm{d}y\\ &=\int_b^x\frac{ab^a}{y^{a+1}}\mathrm{d}y\\ &=b^a\left[-y^{-a}\right]_b^x =1-(x/b)^{-a}. \end{align*}\] したがって，累積分布関数の逆関数は \[ F^{-1}(u)=b/(1-u)^{1/a} \] となり，\(F^{-1}(U)=b/(1-U)^{1/a}\)で生成できる．ただし，\(U\)と\(1-U\)の従う確率分布は同じだから，\(b/U^{1/a}\)で生成できる．

a <- 2.0
b <- 1.0
N <- 1e5
f <- function(x) a*b^a/(x^(a+1))
data.fr <- data.frame(x = b/runif(N)^(1/a))
ggplot(data.fr, aes(x=x))+geom_histogram(aes(y=..density..), binwidth = 0.1, alpha=0.3)+theme_bw()+xlim(1,4)+stat_function(fun=f)

## Warning: Removed 6160 rows containing non-finite values (stat_bin).

## Warning: Removed 2 rows containing missing values (geom_bar).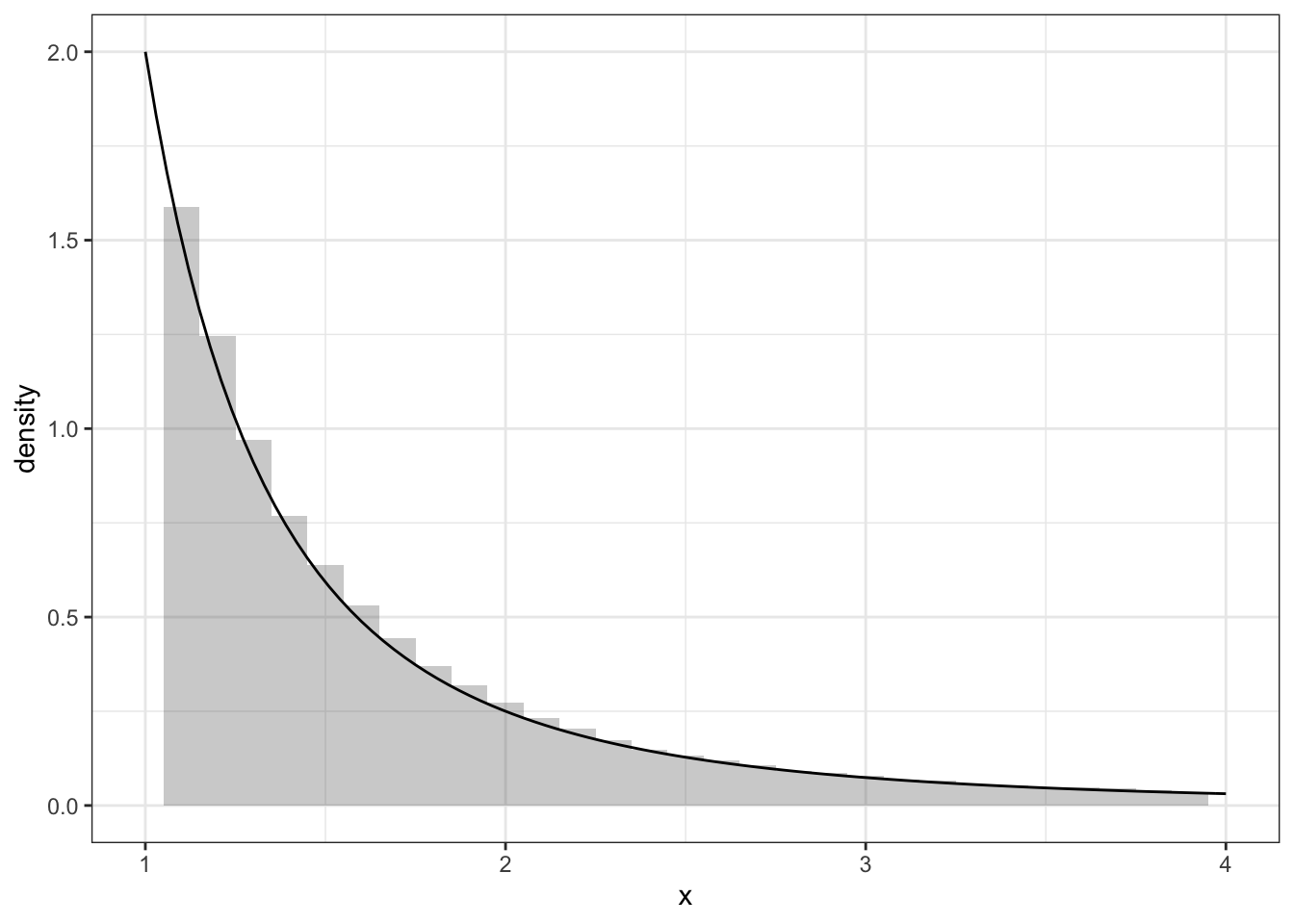

Exercise 2.5 \(\sigma\)は正の実数とする．レイリー分布 (Rayleigh distribution) の確率密度関数は \[ p(x;\sigma)=\frac{x}{\sigma^2}\exp(-x^2/2\sigma^2)\ (x\ge 0) \] で与えられる．R言語の組み込み関数runifを用いてレイリー乱数を生成する方法を記述せよ．

sigma <- 2.0
N <- 1e5
f <- function(x) x/sigma^2 * exp(-x^2/(2*sigma^2))
data.fr <- data.frame(x = sigma*sqrt(-2*log(runif(N))))
ggplot(data.fr, aes(x=x))+geom_histogram(aes(y=..density..),alpha=0.3,binwidth=0.1)+theme_bw()+stat_function(fun=f)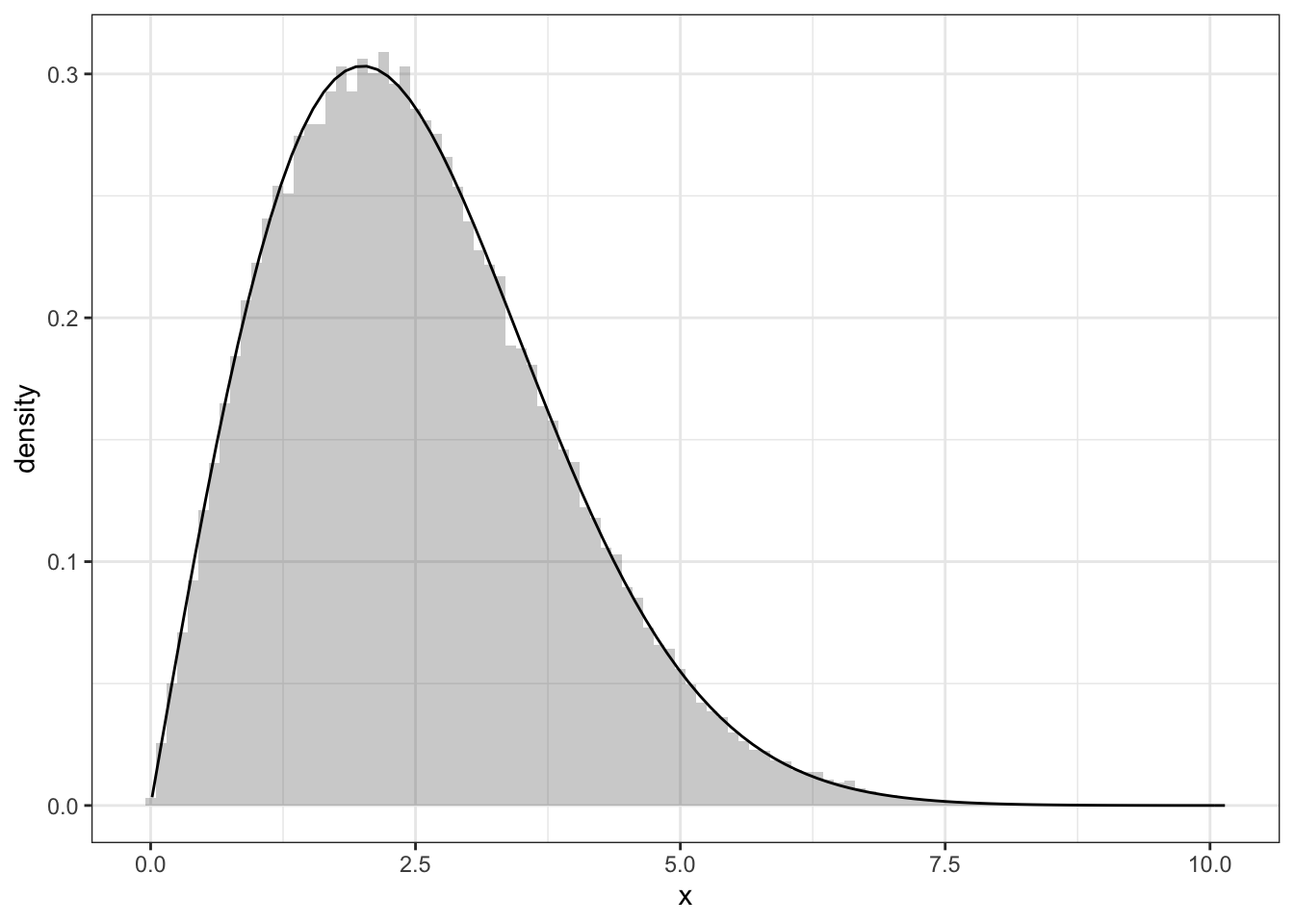

Exercise 2.6 \(a, b\)は正の実数とする．ワイブル分布 (Weibull distribution) の確率密度関数が \[ p(x;a,b)=\frac{a}{b^a}x^{a-1}e^{-(x/b)^a}\ (x\ge 0) \] で与えられる．R言語の組み込み関数runifを用いてワイブル乱数を生成する方法を記述せよ．

a <- 1.5
b <- 2.0
N <- 1e5
f <- function(x) a/b^a*x^(a-1)*exp(-(x/b)^a)
data.fr <- data.frame(x = b*(-log(runif(N)))^(1/a))
ggplot(data.fr, aes(x=x))+geom_histogram(aes(y=..density..),alpha=0.3,binwidth=0.1)+theme_bw()+stat_function(fun=f)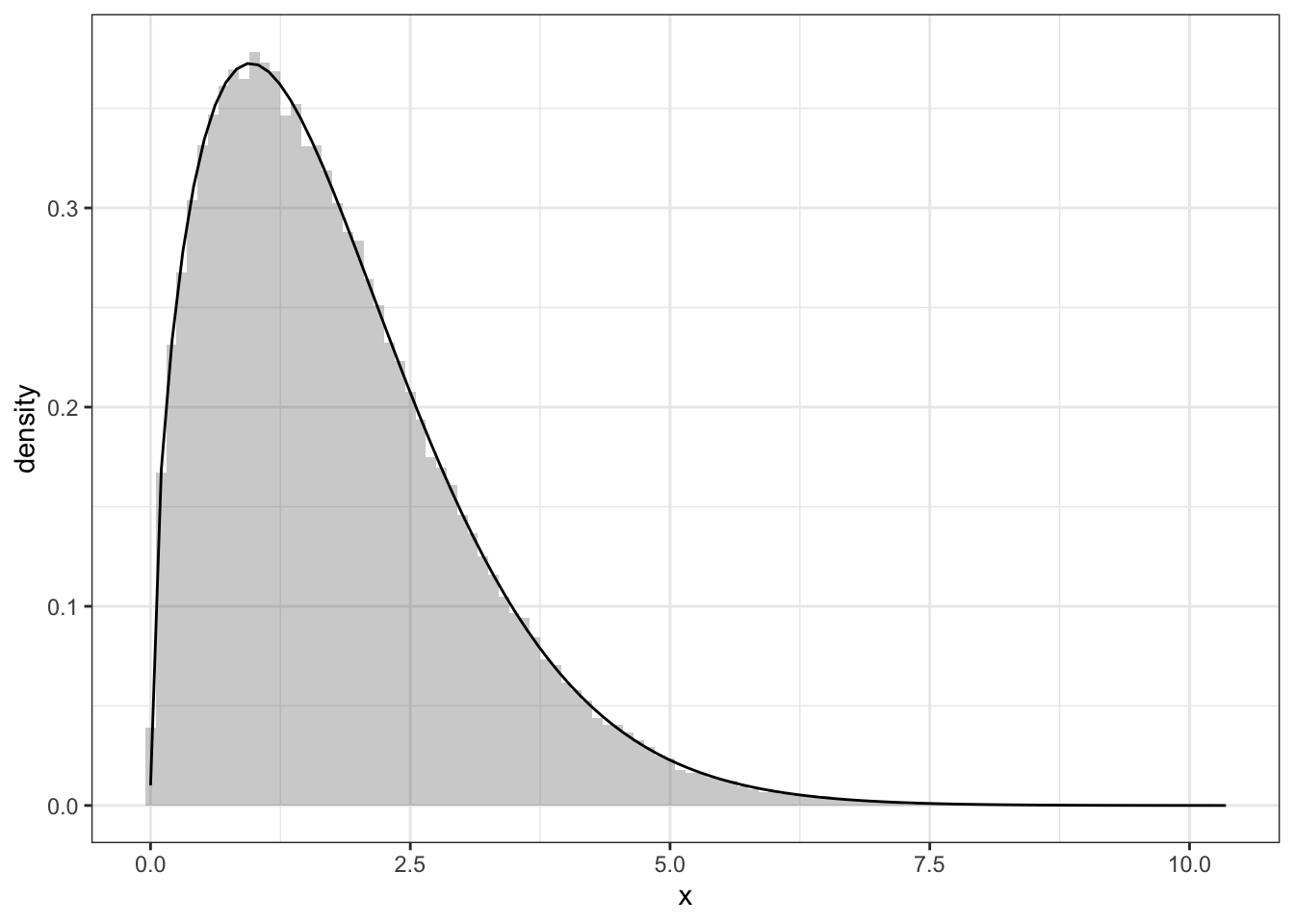

Exercise 2.7 \(N\)は正の整数，\(\theta\)は実数で\(0<\theta<1\)とする．二項分布\(\mathcal{B}(N,\theta)\)の確率関数は \[ p(n; N,\theta)=\binom{N}{n}\theta^n(1-\theta)^{N-n}\ (n=0,\ldots, N) \] で与えられる．R言語の組み込み関数runifを用いて二項分布 に従う乱数を生成する方法を記述せよ．

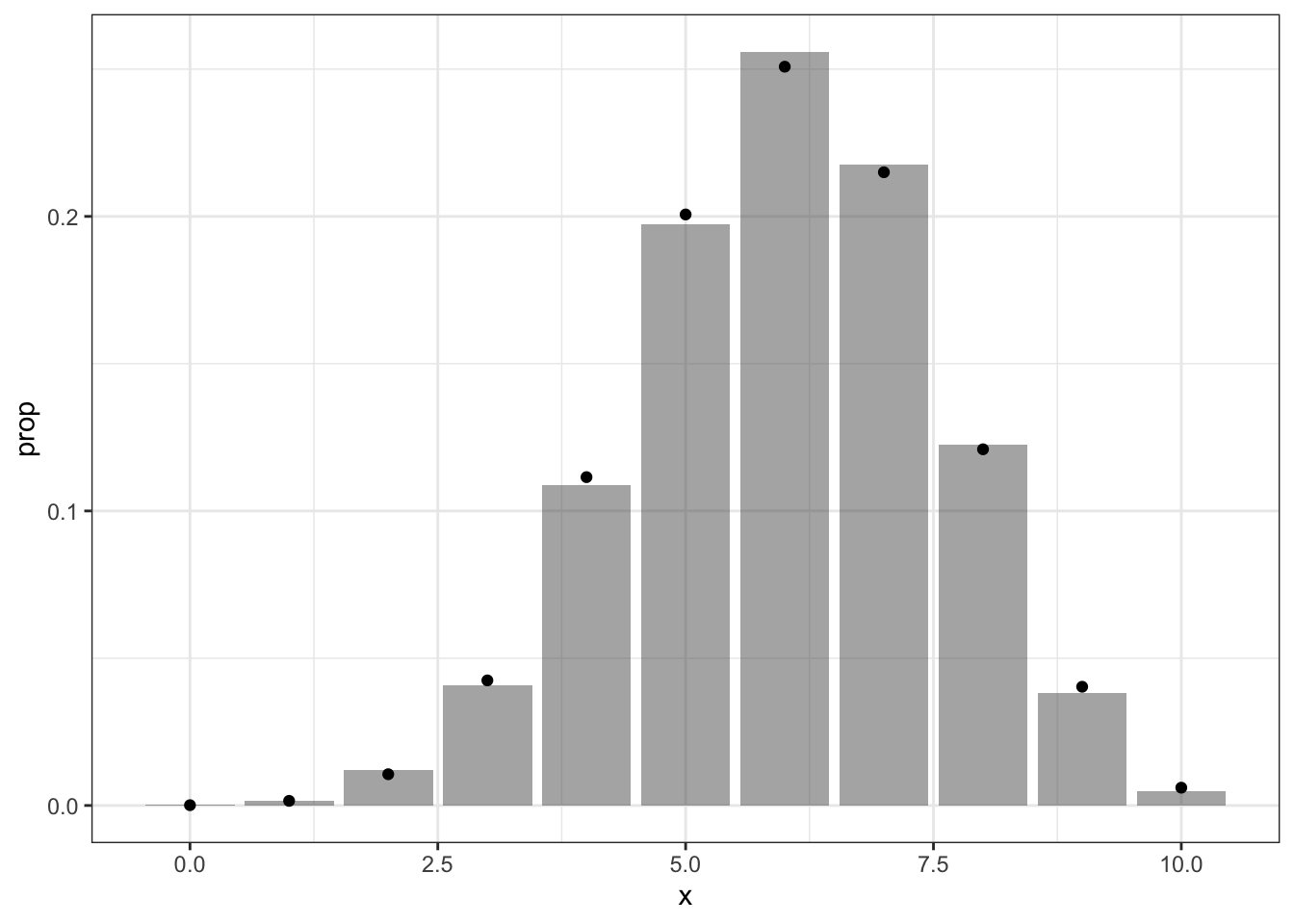
N <- 10
theta <- 0.6
F_seq <- cumsum(dbinom(0:N,N,theta))
f <- Vectorize(function(x) sum(x > F_seq))

data.fr <- data.frame(x=f(runif(1e4)))
ggplot(data.fr, aes(x))+geom_bar(aes(y=..prop..), alpha=0.5)+theme_bw()+stat_function(geom="point", fun=dbinom, args=list(size=N, prob=theta), n=11)