6 メトロポリス・ヘイスティングス法
Exercise 6.1 メトロポリス・ヘイスティングス法の採択関数\(\alpha(x,y)\)の代わりに
\[
\beta(x,y)=\frac{\pi(y)q(y,x)}{\pi(x)q(x,y)+\pi(y)q(y,x)}
\]
を用いても定理6.1，定理6.2と同じ仮定のもと，同じ結論が従うことを示せ．
Solution. メトロポリス・ヘイスティングスカーネルの\(\alpha(x,y)\)を\(\beta(x,y)\)でおきかえたマルコフカーネルを\(P\)と書く． まず定理6.1と同じ結論が従うことをみよう． 定理6.1の証明と同じように， \[ \int_{x\in A, y\in B}\pi(x)q(x,y)\beta(x,y)\mathrm{d}x\mathrm{d}y= \int_{x\in A, y\in B}\pi(y)q(y,x)\beta(y,x)\mathrm{d}x\mathrm{d}y \] を示せば良い．被積分関数に注目すると \[ \pi(x)q(x,y)\beta(x,y)= \frac{\pi(y)q(y,x)\pi(x)q(x,y)}{\pi(x)q(x,y)+\pi(y)q(y,x)} \] となり\(x, y\)について対称な関数であることがわかる．だから，\(x, y\)を入れ替えても同じ値であり，この事実から示したい等式がわかる．したがって\(P\)は\(\Pi\)-対称であり，定理4.8より\(\Pi\)-不変でもある．
つぎに定理6.2を示そう．これについても定理6.2の証明とまったく同じように\(\beta(x,y)>0\ (x,y\in E)\)であることから \[ P(x, A)\ge \int_Aq(x,y)\beta(x,y)\mathrm{d}y=:k(x,y)>0 \] によって定理4.6から結論が従う．よって\(P\)はエルゴード的．
Remark. 本問のように作られたマルコフカーネルを，しばしばバーカーカーネル(See Barker 1965)という．中心極限定理の漸近分散の観点から，バーカーカーネルは必ずメトロポリス・ヘイスティングスカーネルより良くない(See Tierney 1998)．しかし\(\beta(x,y)\)は微分可能性など，関数としてよりなめらかなため，理論的に解析しやすい．
Exercise 6.2 例6.1で紹介された二つの独立型メトロポリス・ヘイスティングス法のそれぞれに対し，式(6.1)で定義される\(M\)を計算せよ．
Solution. 定義から
\[
M=C\sqrt{2\pi}\sup_{x\in\mathbb{R}^d}\frac{1}{1+\theta^2}=C\sqrt{2\pi}.
\]
Exercise 6.3 独立型メトロポリス・ヘイスティングス法を
\(\Pi=\mathcal{N}(0,1)\), \(Q=\mathcal{C}(0,1)\)としたものと，
\(\Pi=\mathcal{C}(0,1)\), \(Q=\mathcal{N}(0,1)\)としたものを実装し，結果を比較せよ．
Solution. 実際に，ふたつのメトロポリス・ヘイスティングス法から，長さ
Nのサンプルを生成し，経路図と採択率，事項相関図を生成してみよう．
N <- 1e5 # No. of iteration
N1 <- 1e3 # No. of iteration for trajectory plot
lag <- 25 # Lag of MCMCs
pi1 <- function(x) dnorm(x) # Target #1
q1 <- function(x) dcauchy(x) # Proposal #1
w1 <- function(x) pi1(x)/q1(x) # Ratio #1
w2 <- function(x) 1/w1(x) # Ratio #2
vec1 <- numeric(N) # Output #1
vec2 <- numeric(N) # Output #2
x0 <- numeric(1) # Initial value
# MCMC #1
x <- x0
for(i in 1:N){
y <- rcauchy(1)
if(runif(1) < w1(y)/w1(x)){
x <- y
}
vec1[i] <- x
}
# MCMC #2
x <- x0
for(i in 1:N){
y <- rnorm(1)
if(runif(1) < w2(y)/w2(x)){
x <- y
}
vec2[i] <- x
}
data.fr <- melt(data.frame(x = c(vec1, vec2), m = rep(1:N,2), method = factor(rep(c(1,2),each=N))), id =c("m","method"))
ggplot(subset(data.fr, m < N1), aes(x = m, y = value, color=method)) + geom_path() + theme_bw() + scale_color_brewer(palette = "Set1") + ggtitle("Trajectory plot")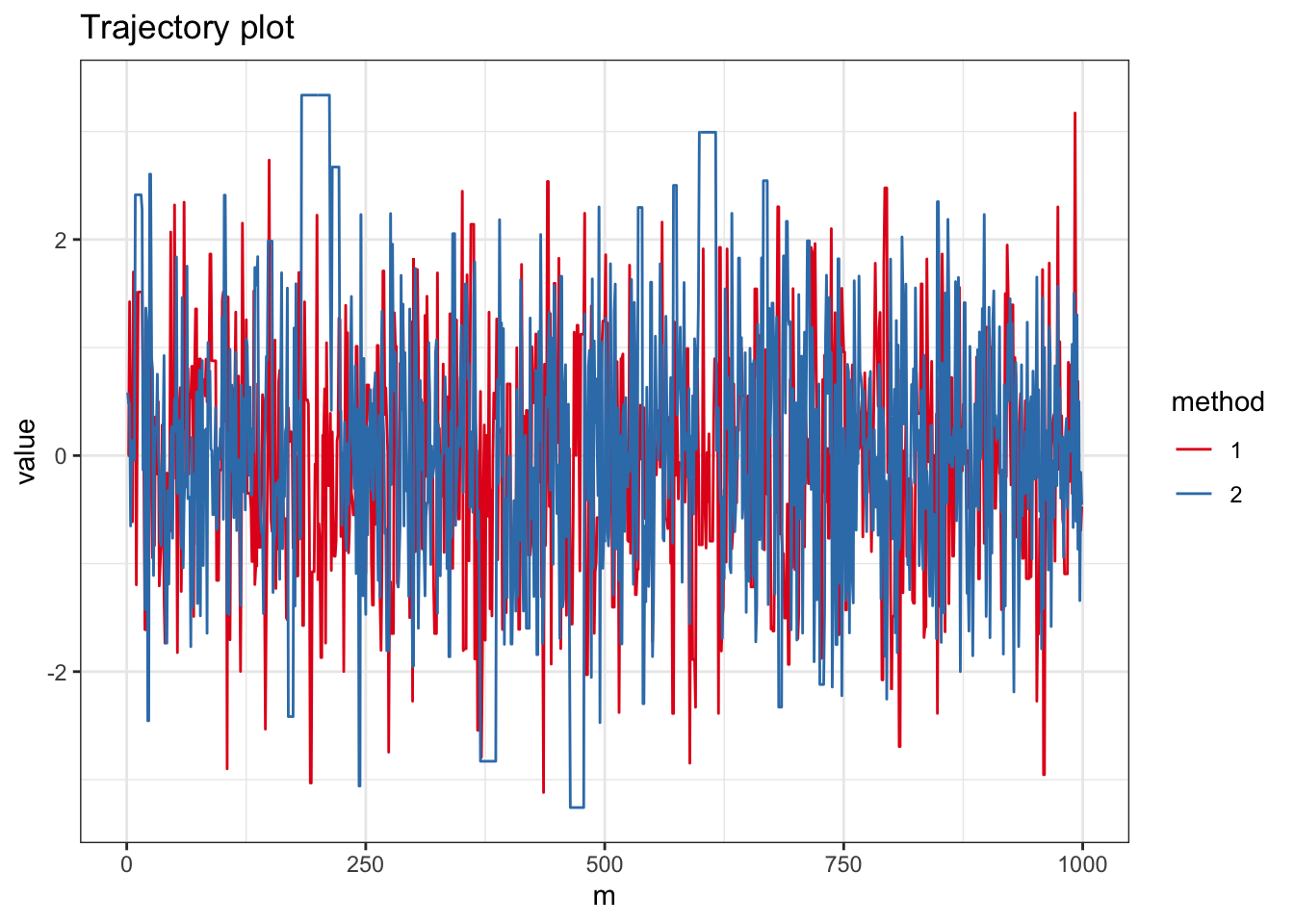
## [1] "Acceptance probability #1 0.70528"## [1] "Acceptance probability #2 0.81821"acf1 <- acf(vec1, lag = lag, plot = FALSE)
acf2 <- acf(vec2, lag = lag, plot = FALSE)
M <- length(acf1$lag)
data.fr <- data.frame(lag = rep(as.vector(acf1$lag),2), y = c(as.vector(acf1$acf), as.vector(acf2$acf)), z = factor(rep(c(1,2), each=M)))
ggplot(data.fr , aes(x = lag, y = y, fill=z)) + geom_bar(stat = "identity", position = position_dodge(), alpha=1.0) + theme_bw() + scale_fill_brewer(palette = "Set1") + ggtitle("Acf plot")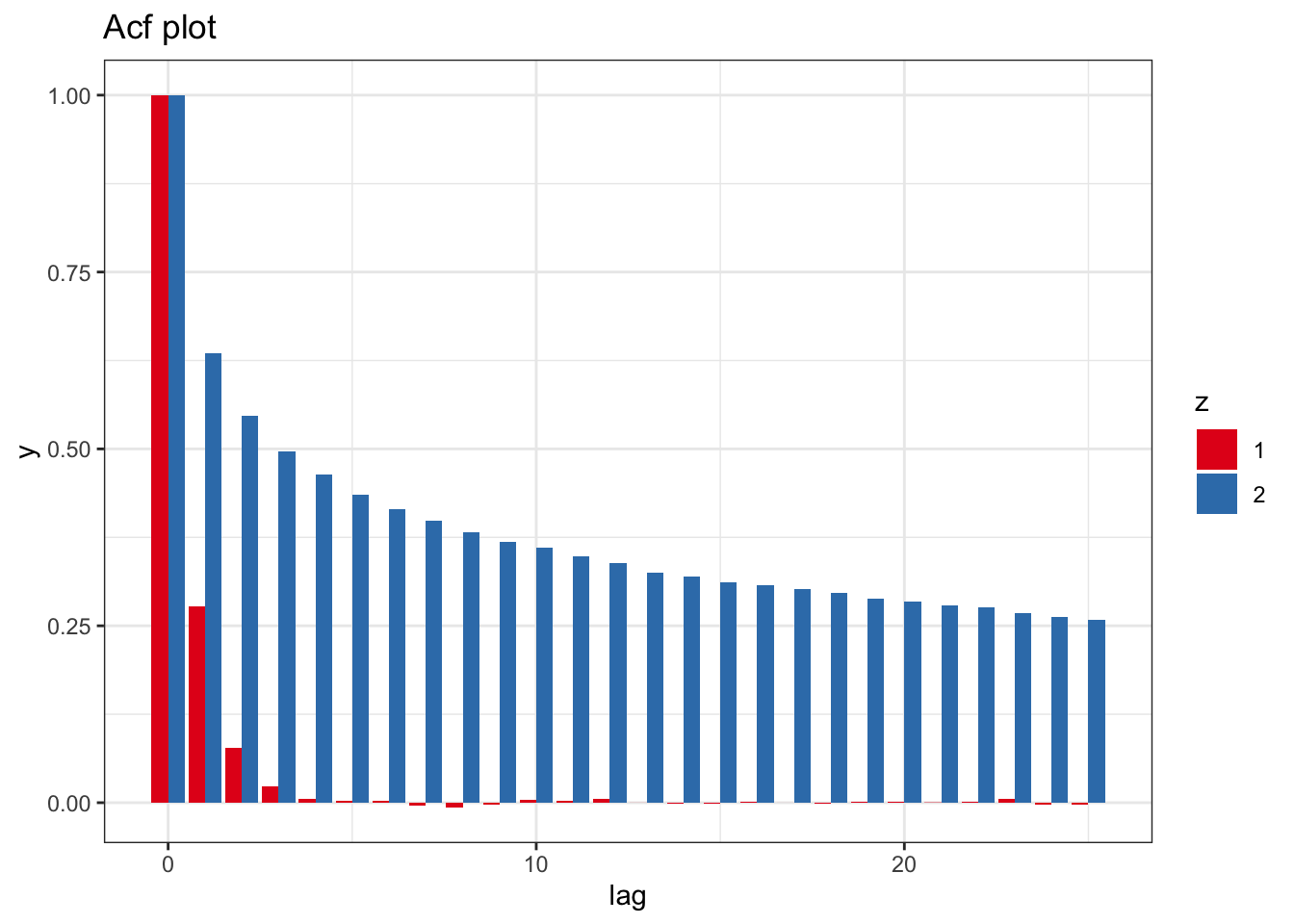
Remark. 前者は一様エルゴード的，後者はそうでないことが知られる．自己相関関数の推移をみるかぎり，理論的な結果と整合的である．
Exercise 6.4 \(\mathbb{R}^d\)上の確率測度\(\Pi\)に対し，確率密度関数\(\pi(x)\)があるとする．メトロポリス・ヘイスティングス法で
正の実数\(\rho,\sigma\)で\(0<\rho<1\)なるものに対し，
\(Q(x,\cdot)=\mathcal{N}(\rho^{1/2}x, (1-\rho)\sigma^2I_d)\)とする．
このとき採択関数が
\[
\alpha(x,y)=\min\left\{1,\frac{\pi(y)\phi_\sigma(x)}{\pi(x)\phi_\sigma(y)}\right\}
\]
で与えられることを示せ．ただし，\(\phi_\sigma(x)\)は\(\mathcal{N}(0,\sigma^2 I_d)\)の確率密度関数とする．
Solution. メトロポリス・ヘイスティングス法の採択関数の定義とみくらべて
\[
\frac{q(y,x)}{q(x,y)}=\frac{\phi_\sigma(x)}{\phi_\sigma(y)}
\]
であること，すなわち
\[
\phi_\sigma(x)q(x,y)=\phi_\sigma(y)q(y,x)
\]
を示せば良い．ただし\(q(x,y)\)は\(Q(x,\cdot)=\mathcal{N}(\rho^{1/2}x, (1-\rho)\sigma^2I_d)\)の確率密度関数
\[
q(x,y)=\frac{1}{\sqrt{2\pi\sigma^2(1-\rho)}}\exp\left(-\frac{(y-\rho^{1/2}x)^2}{2\sigma^2(1-\rho)}\right)
\]
である．いっぽう，
\[\begin{align*}
\phi_\sigma(x)q(x,y)=\frac{1}{2\pi\sigma^2\sqrt{(1-\rho)}}\exp\left(-\frac{x^2+y^2-2\rho^{1/2}xy}{2\sigma^2(1-\rho)}\right)
\end{align*}\]
となり，これは\(x, y\)を入れ替えても同じ値になる．よって\(\phi_\sigma(x)q(x,y)=\phi_\sigma(y)q(y,x)\)が示され，結論が従う．
Remark. 上で紹介したマルコフカーネルは，しばしばpreconditioned Crank-Nikolsonカーネルとよばれ，高次元で，正規分布を事前分布として用いるときの解析に有効である(See Neal 1998, Cotter et al 2013)．関連するアルゴリズムとして，Elliptical slice samplingがある．
Exercise 6.5 定理6.4を証明せよ．
Solution. 定理6.2よりただちにしたがう．なぜなら\(q(x,y)=\gamma(y-x)>0\)となるからだ．
Exercise 6.6 定理6.6を示せ．
Solution. 略
Exercise 6.7 ハミルトン方程式の離散近似は様々な方法がある．
オイラー法は
\[\begin{align*}
x_h&=x_0+h\left(\frac{\partial H}{\partial w}\right)(x_0, w_0), \\
w_h&=w_0-h\left(\frac{\partial H}{\partial x}\right)(x_0, w_0)
\end{align*}\]
で定義される．ただし，正の実数\(h\)はステップ幅．ハミルトニアンが\(H(x,w)=(x^2+w^2)/2\)であるとき，
\[
H(x_h,w_h)-H(x_0, w_0)
\]
を\(H(x_0,w_0)\)を用いて表せ．
Solution. \[\begin{align*}
H(x_h, w_h)-H(x_0,w_0)&=
(x_0+hW_0)^2+(w_0-hx_0)\\
&=(x_0^2+w_0^2)+h^2(x_0^2+w_0^2)\\
&=(1+h^2)H(x_0, w_0)
\end{align*}\]
とあらわせる．
Remark. 上の結果から，オイラー法を繰り返すと，\(k=1,2,\ldots\)にたいし
\[
H(x_{kh},w_{kh})=(1+h^2)^kH(x_0, w_0)
\]
となり，指数的にハミルトニアンが大きくなってしまう．ハミルトニアン方程式の解はハミルトニアンを変えないから，これはオイラー法による近似の誤差がとても大きいことを示している．
Exercise 6.8 同様に修正されたオイラー法では，
ハミルトニアンが\(H(x,w)=(x^2+w^2)/2\)であるとき，
\[
H(x_h,w_h)-H(x_0, w_0)=h^2(-x_0^2+w_h^2)
\]
を示せ．
Solution. 略
Solution. 同様に馬跳び法の場合，ハミルトニアンが\(H(x,w)=(x^2+w^2)/2\)であるとき，
\[
\begin{pmatrix}
x_h\\
w_h
\end{pmatrix}
=A_h \begin{pmatrix}
x_0\\
w_0
\end{pmatrix}
\]
となる行列\(A_h\)を求めよ．
Solution. ３つのステップを行列で表すと，それぞれ \[\begin{align*} \begin{pmatrix} 1&h/2 \\ 0&1 \end{pmatrix}, \begin{pmatrix} 0&1 \\ -h&1 \end{pmatrix}, \begin{pmatrix} 1&h/2 \\ 0&1 \end{pmatrix} \end{align*}\] をひだりから縦ベクトル\((x,w)\)に作用させることに対応する．よって求める行列は \[\begin{align*} \begin{pmatrix} 1&h/2 \\ 0&1 \end{pmatrix}~ \begin{pmatrix} 1&0 \\ -h&1 \end{pmatrix}~ \begin{pmatrix} 1&h/2 \\ 0&1 \end{pmatrix} = \begin{pmatrix} 1-h^2/2&h+h^3/2 \\ -h&1-h^2/2 \end{pmatrix}. \end{align*}\]