Research
About Mathematical Modelling
Nearly 400 years have passed since the founding of modern Western science as the introduction of mathematics into natural science.
Yet the mathematical scientific approach consisting of (1) constructing mathematical models of phenomena using mathematics as a language, (2) examining the properties of the models using the power of modern mathematicsand , (3) comparing the obtained results with reality continues to become increasingly important as a tool for understanding various real-world phenomena, including those related to nature, society, engineering, the environment, and life. In recent years, partly due to the development of computers, mathematical scientific approaches have been used beyond the study of natural phenomena to actively investigate “information phenomena” such as neural networks and “economic phenomena” such as the prediction of stock prices. And this approach continues to dramatically evolve, even today.
The Mathematical Modelling course covers both pure mathematical research into basic equations for fluid motion, basic equations for quantum mechanics, basic equations for heat diffusion in materials, and pure theoretical research for functional and real analyses, as well as practical mathematical models for a wide range of phenomena such as soap flows on a soap bubble film (interfacial and surface flows), air and sea flows, electroporation methods for cancer treatment, and neural networks.
Research groups
The Mathematical Modelling course consists of the Differential Equation Group and the Applied Analysis Group.
Many natural and social phenomena are nonlinear problems, and many of their models involve nonlinear equations that cannot be manually solved, which is why modern mathematical methods are required to investigate the mathematical properties of these models. Both groups engage in the study of mathematical models for various phenomena along with theoretical research involving pure mathematics such as functional analysis, real analysis, and variational analysis as essential tools for model analysis.
The Differential Equation Group engages in mathematical modelling of nonlinear phenomena and theoretical analysis of nonlinear partial differential equations obtained as models for soap flows on a soap bubble film (interfacial and surface flows), air and sea flows, general motion of fluids, and transmission of light in optical fibers.
The Applied Analysis Group conducts a broad range of research into the mathematical aspects of mathematical scientific approaches to phenomena. Phenomena include nonlinear thermal phenomena, general motion of fluids, quantum mechanical phenomena, nonlinear diffusion in fractals, electroporation for cancer treatments, and neural networks.
Differential Equation Group
Mathematical analysis of fluids and gases
The mainstreams of mathematical analysis in hydrodynamics are divided into two: mathematical analysis of compressible fluids originating from the theory of gas dynamics and research into incompressible viscous fluids (Navier-Stokes flow). Over the past 30 years, Japanese academia has led the world in both fields.
Based on these model equations, this research area applies mathematical analysis to elucidate diffusion and wave phenomena.

Analysis of nonlinear waves
This research area deals with special nonlinear wave phenomena that occur in water channels and in signal transmission optical fibers, for example.
These waves vary in travel speed depending on their frequency and possess nonlinear interactions, which cause various phenomena to occur.
This research area is particularly interested in the classification of time-global dynamics of solutions and time-global behavior for the equations found in these phenomena.
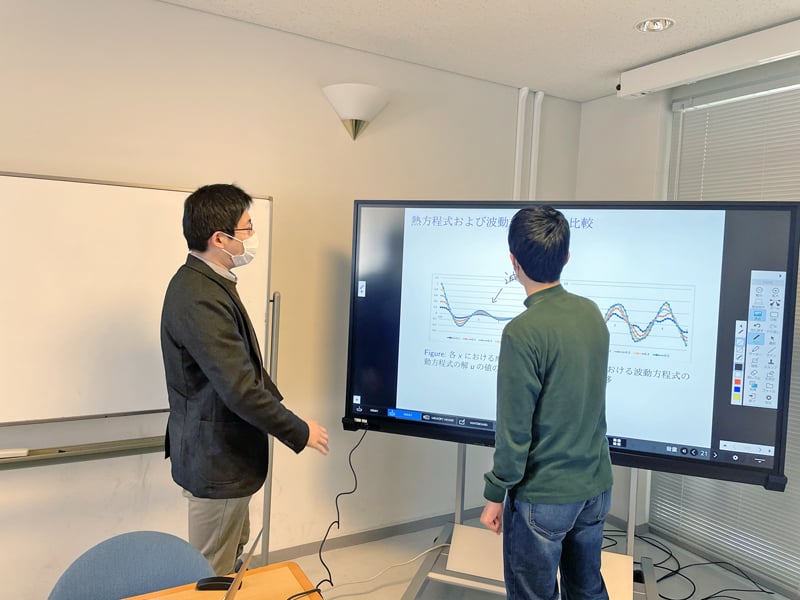
Mathematical modelling of natural phenomena
Large-scale fluids such as the atmosphere and ocean are called global fluids. This research area focuses on global fluid equations for these flows. In recent years, this area has also engaged in mathematical modelling of soap bubbles floating in the atmosphere.
Domain perturbation in hydrodynamics
This research area uses mathematical analysis methods to examine how fluid motion changes as the domain changes in shape.
These studies are relevant to the design of domain shapes when determining the optimal shape of an artificial blood vessel, for example.
Recently, this research area has also been focused on the natural frequency of thin rod-like elastic bodies in addition to those of fluids.
Applied Analysis Group
Analysis of critical phenomena
Although various phenomena exist in reality, a mathematical model of a phenomenon is not the phenomenon itself, which means a phenomenon corresponding to reality does not necessarily exist in the mathematical model itself. For example, for a mathematical model given by a differential equation, we do not know whether a mathematical phenomenon reflecting the real phenomenon exists or not. In other words, the existence of a solution to the equation is not discernible, and must therefore be guaranteed mathematically.
In the language of modern mathematics, “existence” means “compactness.”
One of the research themes in this area is to mathematically investigate what phenomena can occur in the absence of compactness.

In a finite dimensional space, compactness is equivalent to boundedness (Bolzano-Weierstrass theorem) while in an infinite dimensional space many sets of non-compact boundedness can exist. Although it is already known that the series of theories called “profile decomposition” is applicable for this analysis, this research area is focused on applying these theories to the analysis of actual mathematical models.
To date, this area has studied the asymptotic behavior of solutions for critical partial differential equations; the existence of minimization sources for minimization problems associated with critical function inequalities; and the existence and multiplicity of solutions for elliptic equation systems formulated as non-compact variational problems.
The Group’s research fields in mathematical science also include electroporation in cancer treatments and analytical mathematics for neural networks.
Control of time-behavior of incompressible fluids
This research area is interested in the time-global asymptotic behavior of solutions for Navier-Stokes equations that describe the motion of incompressible viscous fluids such as water and oil. Current research is focused mainly on the analysis of kinetic energy decay.
In particular, this research area investigates long-time behaviors of the energy decay with a view to elucidating the nonlinear phenomena of fluids and to controlling fluids with given data.

Mathematical modelling of natural phenomena
Large-scale fluids such as the atmosphere and ocean are called global fluids. This research area focuses on global fluid equations for these flows. In recent years, this area has also engaged in mathematical modelling of soap bubbles floating in the atmosphere.